Lecture 5 - Electron Configurations and Periodic Table Trends

Course

Unit 1

Chapter 2

General Chemistry

Molecular Structure and Properties

Intramolecular and Intermolecular Interactions

This lecture is part of the MEEP curriculum on General Chemistry. Information about Project MEEP and other General Chemistry lectures are available below.

Project MEEP

General Chemistry

Recommended Time: 1.5 Hours

Lecture Preview

What is Chapter 2 of this course about?
How are electrons arranged in an atom?
What are electron configurations, how do we determine them, and how are they important?
What are some periodic table trends and why should we know these trends?

Lecture Content (Part 1)

Welcome to Chapter 2! This chapter talks about intramolecular and intermolecular interactions between chemical structures. In summary, we will discuss the following questions:

How do atoms inside a molecule or compound connect with each other? (Intramolecular, Lectures 6 and 7)
How do molecules or compounds “connect” with each other? (Intermolecular, Lecture 8)
How do those intramolecular and intermolecular interactions determine the molecule’s or compound’s properties? (Applications)

In order to understand how those intramolecular and intermolecular interactions work, we need to understand 1 concept very well. This 1 concept essentially lays out the foundation for these interactions.

Electrons

So, let’s start talking about electrons.

Also, for our convenience, a small widget is added at the bottom right of the screen. When clicked, a periodic table will pop up.

Quantum Theory of Electrons

Recall back in lecture 3, we introduced this diagram (to the right) – a heavily simplified version of a C-12 atom structure. We used the word “heavily simplified” because this diagram doesn’t accurately depict how electrons are actually arranged in an atom. For our purposes, this model is not helpful anymore.

We want to make our model of an atom more accurate because it will immensely help us when we talk about periodic table trends. So, let’s make some adjustments to our model based on discoveries made by scientists.

This newer model is called the quantum theory of electrons.

This diagram is actually not accurate for our purposes now.

Main Idea: Electrons contain energy. Electrons occupy orbitals. Orbitals can be described by 4 values. By knowing these 4 values, we can know the specific orbital the electron resides in.

Let’s start introducing these 4 values.

1. The Principle Quantum Number

The principle quantum number tells us which shell an electron resides in.

The principle quantum number $n$ basically tells us the general size and energy levels of the orbital this electron resides in. It’s also called the shell. Think of it as a label for the neighborhood the electron lives in.

The higher the number, the farther away the electron is from the nucleus. The farther away the electron is from the nucleus, the higher energy it contains.

The farthest an electron can reside in depends on the period of the element. For example:

the element carbon $C$ can house electrons at $n = 1 \text{ and } 2$ because carbon is at period 2.
The element rubidium $Rb$ can house electrons at $n = 1, 2, 3, 4, \text{ and } 5$ because rubidium is at period 5.

2. The Secondary Quantum Number

The secondary quantum number $l$ basically tells us, given the shell the electron is in, the shape of the orbital the electron resides in (called the subshell). Think of it as a street – 1st street, 2nd street, etc. within the neighborhood. The streets take on very interesting shapes.

$l$ is dependent on $n$ . It starts from $0$ and ends at $n-1$ . We can interpret it as “the bigger the neighborhood, the more streets there are”. The subshells (streets) have names:

Orbital shells and subshells with relation to the period the element is in. Attribution: Pellegatta Simone, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

If $l = 0$ , then it’s an $s$ subshell, which consists of $s$ orbitals.
If $l = 1$ , then it’s a $p$ subshell, which consists of $p$ orbitals.
If $l = 2$ , then it’s a $d$ subshell, which consists of $d$ orbitals.
If $l = 3$ , then it’s an $f$ subshell, which consists of $f$ orbitals.
There are $g, h, i$ -subshells for $l = 4, 5, 6$ , respectively, but it’s way beyond scope.
The higher the $l$ value, the higher energy level the electron has.

We prefer using s, p, d, f over $l$ values.

Essentially, the shapes of orbitals (subshells) are determined by the shell the electron resides in. For example:

The element carbon can house electrons in shells .
- At $n = 1$ , electrons can reside at $l = 0$ (s subshell).
- At $n = 2$ , electrons can reside at $l = 0, 1$ (s and p subshells).
The element rubidium can house electrons in shells .
- At $n = 1$ , electrons can reside at $l = 0$ (s subshell).
- At $n = 2$ , electrons can reside at $l = 0, 1$ (s and p subshells).
- At $n = 3$ , electrons can reside at $l = 0, 1, 2$ (s, p, and d subshells).
- At $n = 4$ , electrons can reside at $l = 0, 1, 2, 3$ (s, p, d, and f subshells).
- At $n = 5$ , electrons can reside at $l = 0, 1, 2, 3, 4$ (s, p, d, f, and g subshells).

3. The Magnetic Quantum Number

The magnetic quantum number $m_l$ basically tells us, given the shell and the shape of the orbital, the orientation of the orbital the electron resides in. Think of it as a house address (orientation) at a street (shape) in a neighborhood (shell).

The orientations (house) of the orbitals are interesting.

The number of orientations for an orbital is determined by the shape of the orbital. In other words, the $m_l$ value is determined by the $l$ value. the $m_l$ value starts at $-l$ and ends at $+l$ .

If the electron is in the s orbital ( $l = 0$ ), the $m_l$ values can be $0$ .
If the electron is in the p orbital ( $l = 1$ ), the $m_l$ values can be $-1, 0, 1$ .
If the electron is in the d orbital ( $l = 2$ ), the $m_l$ values can be $-2, -1, 0, 1, 2$ .
If the electron is in the f orbital ( $l = 3$ ), the $m_l$ values can be $-3, -2, -1, 0, 1, 2, 3$ .

To summarize, electrons reside in orbitals with specific shape with specific orientation in a specific shell.

These are orientations and shapes of electron orbitals. Modified from https://commons.wikimedia.org/wiki/File:Single_electron_orbitals.jpg

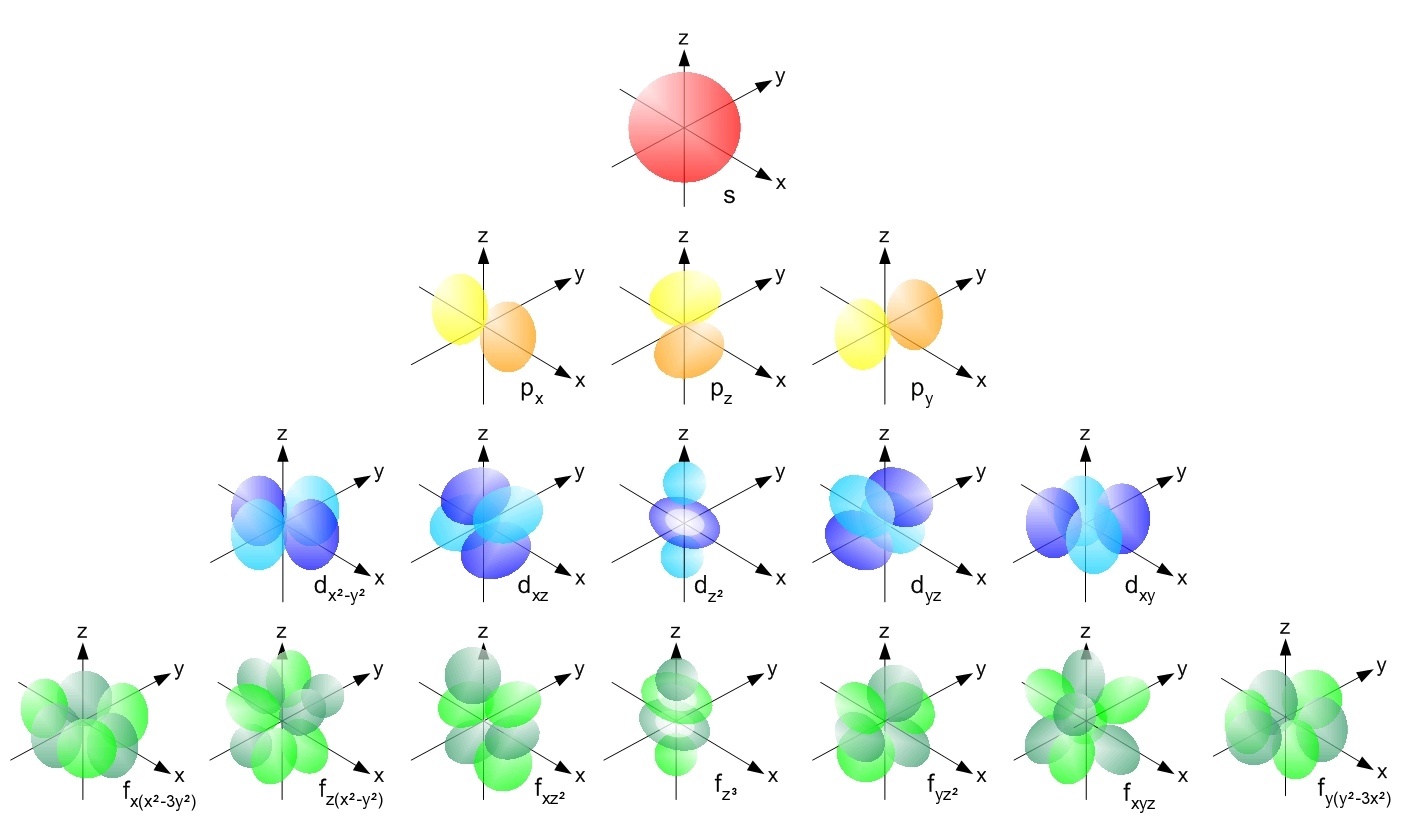
Realistically speaking, we only need to remember what s and p orbitals look like and their possible orientations.

4. The Spin Quantum Number

We talked about how electrons can live in a neighborhood (shell, $n$ ), in a street (shape $l$ ), and inside a house (orientation, $m_l$ ). The last value $m_s$ tells us the spin of the electron. Simply speaking, each house can only house 2 electrons max – one on the lower floor, and one on the higher floor.

The electron residing in the lower floor has $m_s = -1/2$ .
The electron residing in the upper floor has $m_s = +1/2$ .

Scientifically, the values denote the spin of the electron – an intrinsic electron property that can be detected using advanced technologies. However, this is more modern physics than general chemistry, so we will just glance over it. The only important takeaway from this value is that: If there are 2 electrons occupying in the same orbital, they have to have opposite spin.

Quick Summary

Here is a video about how those quantum numbers can be visualized by minutephysics. Pay attention to the quantum numbers at the corner of the video when the narrator is going through the models.

Here’s also a Wikimedia Commons gallery that has orbital models labeled with quantum numbers. Below are some models with quantum numbers labeled $(n, l, m_l)$ . Click here for attributions.

https://commons.wikimedia.org/wiki/Hydrogen_orbitals_3D

To summarize, the quantum theory of electrons utilizes 4 numbers to pinpoint the approximate location of an electron. It also tells us the location, shape, position, and electron spin within the orbitals. Let’s organize the information.

an subshell can house 2 electrons.
- It is because that s orbitals have $l = 0$ , which allows 1 orientation $m_l = 0$ . Since each orientation can house 2 electrons, each s subshell can house $2\times 1 = 2$ electrons.

a subshell can house 6 electrons.
- It is because that p orbitals have $l = 1$ , which allows 3 orientations $m_l = -1, 0, 1$ . Since each orientation can house 2 electrons, each p subshell can house $2\times 3 = 6$ electrons.

a subshell can house 10 electrons.
- It is because that d orbitals have $l = 2$ , which allows 5 orientations $m_l = -2, -1, 0, 1, 2$ . Since each orientation can house 2 electrons, each d subshell can house $2\times 5 = 10$ electrons.

an subshell can house 14 electrons.
- It is because that f orbitals have $l = 3$ , which allows 7 orientations $m_1 = -3, -2, -1, 0, 1, 2, 3$ . Since each orientation can house 2 electrons, each f subshell can house $2\times 7 = 14$ electrons.

Practically speaking, for this class, we only need to remember this summary to heart. The explanations above more or less elaborate the concepts. If you are interested in physical chemistry, familiarization with the quantum numbers is highly recommended. Why we are so adamant about learning this is that we can understand how the diagram below is created.

This is the energy level diagram for electron orbitals, and this is very important. The relative position of each orbital is experimentally measured and determined. And through this diagram, we can finally talk about electron configuration.

Electron Configuration

Before we start talking about it, let’s quickly go through some notation. In electron configuration notation, we have 3 components.

The principle quantum number of the electron.
The letter that designates the subshell.
A superscript number that tells us how many electrons are occupying in that particular subshell.

For example, if we say $3d^5$ , it means that there are 5 electrons occupying in the $d$ subshell at shell 3.

Filling in the Electrons

In an ideal world, we would assume electrons fill in the subshells like so:

$1s \rightarrow 2s \rightarrow 2p \rightarrow 3s \rightarrow 3p \rightarrow 3d \rightarrow 4s \rightarrow 4p \rightarrow 4d \rightarrow 4f \rightarrow 5s \rightarrow 5p...$

However, if we remember our quantum number analogy, we would realize that quantum numbers are more or less from a “city planning” perspective. Electron occupation, on the other hand, is more or less from a “what actually happens” perspective. In other words, how electrons move in to the houses is not what we would expect.

In reality, electrons fill in the subshells like so:

$1s \rightarrow 2s \rightarrow 2p \rightarrow 3s \rightarrow 3p \rightarrow 4s \rightarrow 3d \rightarrow 4p \rightarrow 5s \rightarrow 4d \rightarrow 5p \rightarrow 6s...$

As we can see, it seems very weird. However, we can somehow squeeze out a pattern here.

Observe the energy level diagram. We realize that the electrons fill in from lowest to highest energy. Because the $3d$ orbitals have higher energy than the $4s$ orbitals, the electrons will occupy $4s$ orbitals first and then the $3d$ ones.
The same explanation can be used for $4f$ orbitals and $6s$ orbitals – $4f$ orbitals have higher energy compared to the $6s$ ones, so the $6s$ orbitals get filled first, and then the $4f$ ones.
The diagram to the right essentially describes the energy level pattern.

The 3 Rules of Electron Configuration

The pattern we discussed above is one of the rules of electron configuration. Here are some other rules (including the one we just discussed). The rules should be on the more intuitive side.

Rule 1 – The Energy Rule (a.k.a the Aufbau Principle):

When filling an atom’s orbitals with electrons, start with the lowest energy level and progressively move to higher energy levels. Essentially, electrons want to live near to the nucleus and will occupy houses that are the lowest energy and available. (see the energy level diagram again)

Rule 2 – The Exclusion Rule (a.k.a the Pauli Exclusion Principle):

No two electrons in an atom can have the same set of quantum numbers, meaning if two electrons occupy the same orbital, they must have opposite spins (one spin up, one spin down). Essentially, each house can accommodate up to 2 electrons, 1 living on the lower floor and 1 living on the upper floor – no 2 electrons can live in the same floor.

Rule 3 – The Single Occupancy Rule (a.k.a the Hund’s Rule):

When filling orbitals within a subshell (like 2p), each orbital must be occupied with one electron before any orbital is doubly occupied, and all electrons in singly occupied orbitals should have the same spin. Essentially, if there are houses “equidistant” from the nucleus, electrons will preferably move to the empty houses first.

And as tradition, there are exceptions to these rules because the exceptions somehow make the atom even more stable.

Electron Configurations for Elements 1-36

Using these 3 rules, let’s start writing the electron configurations of atoms.

Electron Configuration: Elements 1-20

The animation to the right describes how we can fill in the electrons for elements 1-20. The chemical symbol, atomic number, number of electrons, energy level diagram, and electron configuration of that element is included.

Try to get a general idea of how electrons are filled because we will do elements 21-40 next.

$H: 1s^2$

$He: 1s^2$

$Li: 1s^2 2s^1$

$Be: 1s^2 2s^2$

$B: 1s^2 2s^2 2p^1$

$C: 1s^2 2s^2 2p^2$

$N: 1s^2 2s^2 2p^3$

$O: 1s^2 2s^2 2p^4$

$F: 1s^2 2s^2 2p^5$

$Ne: 1s^2 2s^2 2p^6$

$Na: 1s^2 2s^2 2p^6 3s^1$

$Mg: 1s^2 2s^2 2p^6 3s^2$

$Al: 1s^2 2s^2 2p^6 3s^2 3p^1$

$Si: 1s^2 2s^2 2p^6 3s^2 3p^2$

$P: 1s^2 2s^2 2p^6 3s^2 3p^3$

$S: 1s^2 2s^2 2p^6 3s^2 3p^4$

$Cl: 1s^2 2s^2 2p^6 3s^2 3p^5$

$Ar: 1s^2 2s^2 2p^6 3s^2 3p^6$

$K: 1s^2 2s^2 2p^6 3s^2 3p^6 4s^1$

$Ca: 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2$

Remember: $3d$ has a higher energy than $4s$ , thus we go for $4s$ first. However, having a higher energy doesn’t mean it’s actually farther from the nucleus.

Subshell $3d$ has a higher energy than subshell $4s$ .
Subshell $3d$ is closer to the nucleus than subshell $4s$ because it’s still $n = 3$ rather than $n = 4$ .

Also, as we can see, the configurations are getting a bit long and bulky. We can actually abbreviate those. We simply take an element and look for its nearest noble gas (Group 18) below it. We then replace the bulky configurations with the noble gas in brackets and write the rest that aren’t covered by the noble gas configuration. So, the electron configurations for elements 1-20 can be rewritten into:

$H: 1s^2$

$He: 1s^2$

$Li: 1s^2 2s^1$

$Be: 1s^2 2s^2$

$B: 1s^2 2s^2 2p^1$

$C: 1s^2 2s^2 2p^2$

$N: 1s^2 2s^2 2p^3$

$O: 1s^2 2s^2 2p^4$

$F: 1s^2 2s^2 2p^5$

$Ne: 1s^2 2s^2 2p^6$

$Na: [Ne] 3s^1$

$Mg: [Ne] 3s^2$

$Al: [Ne] 3s^2 3p^1$

$Si: [Ne] 3s^2 3p^2$

$P: [Ne] 3s^2 3p^3$

$S: [Ne] 3s^2 3p^4$

$Cl: [Ne] 3s^2 3p^5$

$Ar: [Ne] 3s^2 3p^6$

$K: [Ar] 4s^1$

$Ca: [Ar] 4s^2$

This notation focuses on what is happening on the outer shell and the higher energy levels. For our purposes, it’s important because chemical interactions almost always involve outer shell electrons moving. The bulkier notation takes away focus from outer shells, but we will use both in appropriate contexts.

Also, it is best to know the electron configurations of elements 1-20 by heart or at least be familiar with it.

Electron Configuration: Elements 21-36

For elements 21-36, we will use the abbreviated notation. It’s also around here, we start to see some exceptions to the 3 rules of electron configurations.

As we watch the animation to the right, pay attention to the exceptions and take note on why this is an exception.

A general rule to why exceptions occur is that the atom or molecule discovers a state that makes them even stabler.

Here, we encountered some exceptions – chromium $Cr$ and copper $Cu$ .

Chromium (24)

Expected: $[Ar] 3d^4 4s^2$

Reality: $[Ar] 3d^5 4s^1$

Copper (29)

Expected: $[Ar] 3d^9 4s^2$

Reality: $[Ar] 3d^{10} 4s^1$

What happened here is that half-filled or fully-filled d or f subshells are generally more stable compared to other configurations. Other exceptions that follow the same logic include:

Molybdenum (42)

Expected: $[Kr] 4d^4 5s^2$

Reality: $[Kr] 4d^5 5s^1$

Palladium (46)

Expected: $[Kr] 4d^8 5s^2$

Reality: $[Kr] 4d^{10}$

Silver (47)

Expected: $[Kr] 4d^9 5s^2$

Reality: $[Kr] 4d^{10} 5s^1$

The palladium example is more unpredictable because its 5s subshell is emptied to fully fill the 4d subshells. As we go on the periodic table, the configuration exceptions get more and more unpredictable. As the atom becomes larger, more electron interactions are available, which means more potential ways to be stabler. So, we will usually provide the electron configuration for elements with higher atomic numbers.

We can also see a pattern of subshell presence and periodic table location:

Elements in groups 1-2 tend to have s subshell activity.
Elements in groups 13-18 tend to have p subshell activity.
Elements in groups 3-12 (transition metals) tend to have a lot of d subshell activity.
Elements in the La-Ac groups tend to have a lot of f subshell activity.

As a result, we can categorize the periodic table with respect to orbital subshell activity. We can see this in the periodic table provided (the widget at the bottom right) – at the bottom left of the periodic table, there is an “electron configuration blocks” section that groups elements in terms of subshell activity.

Groups 1-2 correspond to s-block.
Groups 13-18 correspond to p-block (except $He$ ).
Groups 3-12 correspond to d-block.
La-Ac groups correspond to f-block.

Valence Electrons

As we have mentioned before, it’s usually the outer shell electrons that participate in atomic and molecular interactions. They are so important, in fact, that we have a name for those electrons.

Valence electrons are electrons that occupy the outermost shell orbitals. For elements in the d- and f-blocks, the d and f subshells (respectively) are counted as valence electrons as well, despite being at a lower shell orbital, due to their involvement in chemical reactivity.

For s-block elements, they may contain 1-2 valence electrons.

For p-block elements, they may contain 3-8 valence electrons. (p subshell can contain up to 6 electrons)

For d-block elements, they may contain 3-12 valence electrons. (d subshell can contain up to 10 electrons)

For f-block elements, they may contain 3-16 valence electrons. (f subshell can contain up to 14 electrons)

If an atom or molecule reacts or interacts with a substance or an environment without changing its atomic number, it almost always the valence electrons that are responsible for those reactions or interactions.

Below is a table listing the element and its corresponding number of valence electrons.

Red is s-block; yellow is p-block; blue is d-block; and green is f-block. Adapted from https://en.wikipedia.org/wiki/Valence_electron

Let’s quickly make some sense out of it.

Carbon has an electron configuration of .
- Its outermost shell is $n = 2$ , which hosts 4 electrons. Thus, it has 4 valence electrons.

Potassium has an electron configuration of .
- Its outermost shell is $n = 4$ , which hosts 1 electron. Thus, it has 1 valence electron.

Copper has an electron configuration of .
- Its outermost shell is $n = 4$ , which hosts 1 electron.
- Copper is a d-block element, so we count the highest d subshell (3d in this case) as well, which hosts 10 electrons.
- Thus, it has 11 valence electrons.

Palladium has an electron configuration of .
- Its outermost shell is considered to be $n = 5$ (because 2 electrons were moved from 5s to 4d for stability), which host 0 electrons.
- Palladium is a d-block element, so we count the highest d subshell (4d in this case) as well, which hosts 10 electrons.
- Thus, it has 10 valence electrons.

Again, the reason we want to know about valence electrons is that reactivity and interactivity of an element is highly tied to valence electrons and, in turn, electron configurations.

Visualizing Valence Orbitals

To really hammer in electron configurations, let’s visualize those orbitals. We will only visualize the orbitals for valence electrons since they are at the outermost shell. Other core (non-valence) electrons are covered by the valence electron orbitals.

Recall the shape of s, p, d, and f subshells. We will only focus on s and p subshells.

Subshell shapes of 1s, 2p, 3d, and 4f. We only need to remember s and p subshells. Attribution: haade, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons

Example 1: Visualization of Period 1 Element Orbitals

There are only 2 elements in period 1 – hydrogen and helium. Their valence electron configuration is also quite simple, being $1s^1, 1s^2$ respectively.

Now let’s focus on the 2nd period, where the p-block is introduced.

Example 2: Visualization of Period 2 Element Orbitals

So, the valence electrons are $2s^1, 2s^2, 2s^2\ 2p^1, 2s^2\ 2p^2, 2s^2\ 2p^3, 2s^2\ 2p^4, 2s^2\ 2p^5, 2s^2\ 2p^6$ respectively. Let’s see how the addition of p-orbitals can change the orbitals of electrons.

Let’s first look at $Li, Be$ , which only has s-orbitals. So, the valence electron orbitals for $Li, Be$ should be similar to that of $H, He$ .

Let’s look at the rest of the period 2 elements – $B, C, N, O, F, Ne$ .

The yellow orbitals are p-orbitals with specific orientation.

Try to connect the visualizations to the atomic orbital diagrams. Half-filled orbitals are reflected as 1 electron occupying the p-orbitals. Fully filled orbitals are reflected as 2 electrons occupying the p-orbitals.

Half-filled orbitals will be discussed in the next lecture.

This visualization generally holds true for elements of similar valence electron configuration. We won’t be visualizing elements with d-orbitals (like transition metals) because if we look at the orientations of d-orbitals, the visualization gets incredibly messy.

Ions and Oxidation States

Ions are basically atoms with different number of electrons compared to protons. However, not all elements have a stable ionic form, such as the noble gases. And for those that can have ionic forms, not all ionic forms are stable – some ionic forms are more common than others.

Oxidation states, on the other hand, cover a bit more than ions. Oxidation states can answer these 2 questions.

If this element is participating in an ionic interaction, what charge would it have?
If this element isn’t participating in an ionic interaction, what charge would it have if we assume it’s an ionic interaction?

Using electron configurations, we can explain how some ions and oxidation states are more common than others, although sometimes this model falls short for some, such as $Cu (II)$ .

Here are some important patterns when it comes to ion formation.

If an element gains electrons to be negatively charged (anion), it follows the electron configuration rules (and exceptions).
If an element loses electrons to be positively charged (cation), the electrons farthest from the nucleus leave first, not the electrons with the highest energy.

The reason an element may gain or lose electrons to become ions is that the ions are stable enough to exist. However, stability of an element is determined by a multitude of factors, which includes:
- The electron configuration of the ion.
- The interactions of the ion and the environment.
- Potential reactions the ion can have with itself or the environment.
- etc.

Let’s look at some examples.

Noble Gases

Noble gases are easy to understand. If an element has an electron configuration that ends in $\text{n} p^6$ , we can (rest assured) that they will be extremely stable. They are so stable that it’s difficult to gain or lose electrons. Helium is an exception with $1s^2$ , but it’s still a noble gas.

The following elements are noble gases and their electron shell diagrams (excluding radon).

$He: 1s^2$

$Ne: 1s^2\ 2s^2\ 2p^6$

$Ar: [Ne]\ 3s^3\ 3p^6$

$Kr: [Ar]\ 3d^{10}\ 4s^2\ 4p^6$

$Xe: [Kr]\ 4d^{10}\ 5s^2\ 5p^6$

$Rn: [Xe]\ 4f^{14}\ 5d^{10}\ 6s^2\ 6p^6$

Attribution: Pumbaa (original work by Greg Robson), CC BY-SA 2.0 UK https://creativecommons.org/licenses/by-sa/2.0/uk/deed.en, via Wikimedia Commons

This type of electron configuration that noble gases have is called a closed-shell configuration, because it’s not open to change.

Example 1: Noble Gases in Medicine

This extremely stable configuration is why noble gases are very unreactive. Their unreactive-ness has useful applications, which is making sure nothing reacts. For example:

Helium $He$ can be used in laparoscopic surgery – a minimally invasive procedure that looks inside our stomach or pelvis. Gas is pumped alongside the surgical instruments to make our organs easier to see on the monitor. Carbon dioxide $CO_2$ is used sometimes, but helium provides a better alternative because:

$CO_2$ can enter the bloodstream and participate with our blood bicarbonate buffering system and potentially increase the acidity of our blood, leading to acidosis. $He$ is so inert that it cannot interact with anything in our blood, preventing potential acidosis.

Xenon $Xe$ can be used as anesthesia because it binds to neurons and inactivate them. However, other substances can be used to inactivate neurons. Xenon is particularly of interest is because:

It has cardiovascular stabilizing properties.
It has rapid onset and emergence from anesthesia.
It cannot be metabolized by our system because xenon is highly unreactive.

Alkali Metals and Alkaline Earth Metals

Alkali metals are group 1 and alkaline earth metals are group 2.

These groups are also easy to understand. Let’s observe their electron configurations and see if they can gain or lose electrons. We can check the periodic table as well to see where they are.

We will ignore elements that are near the end – their properties aren’t known yet because they are so unstable.

Alkali Metals

$Li: 1s^2\ 2s^1$

$Na: [Ne]\ 3s^1$

$K: [Ar]\ 4s^1$

$Rb: [Kr]\ 5s^1$

$Cs: [Xe]\ 6s^1$

$Fr: [Rn]\ 7s^1$

Alkaline Earth Metals

$Be: 1s^2\ 2s^2$

$Mg: [Ne]\ 3s^2$

$Ca: [Ar]\ 4s^2$

$Sr: [Kr]\ 5s^2$

$Ba: [Xe]\ 6s^2$

$Ra: [Rn]\ 7s^2$

As we can see, alkali metals and alkaline earth metals have a very distinct pattern:

Alkali metals have 1 valence electron.
Alkaline earth metals have 2 valence electrons.
If they lose all their valence electrons, they will have the same electron configuration as that of noble gases (a closed shell configuration), which is very stable.

So, if those elements become ions, they will most likely be:

Alkali Metal Ions

$Li^+: 1s^2$

$Na^+: [Ne]$

$K^+: [Ar]$

$Rb^+: [Kr]$

$Cs^+: [Xe]$

$Fr^+: [Rn]$

Alkaline Earth Metal Ions

$Be^{2+}: 1s^2$

$Mg^{2+}: [Ne]$

$Ca^{2+}: [Ar]$

$Sr^{2+}: [Kr]$

$Ba^{2+}: [Xe]$

$Ra^{2+}: [Rn]$

We can also conclude the following:

Alkali metals have an oxidation state of +1.
Alkaline earth metals have an oxidation state of +2.

Using the same reasoning, we can conclude that $Al$ , when it becomes an ion, will be $Al^{3+}$ .

Chalcogens and Halogens

Now, let’s look at the other end of the periodic table (groups 16 and 17). Some noble gases are included for reference.

Chalcogens:

$O: 1s^2\ 2s^2\ 2p^4$

$S: [Ne]\ 3s^2\ 3p^4$

$Se: [Ar]\ 3d^{10}\ 4s^2\ 4p^4$

$Te: [Kr]\ 4d^{10}\ 5s^2\ 5p^4$

$Po: [Xe]\ 4f^{14}\ 5d^{10}\ 6s^2\ 6p^4$

Halogens:

$F: 1s^2\ 2s^2\ 2p^5$

$Cl: [Ne]\ 3s^2\ 3p^5$

$Br: [Ar]\ 3d^{10}\ 4s^2\ 4p^5$

$I: [Kr]\ 4d^{10}\ 5s^2\ 5p^5$

$At: [Xe]\ 4f^{14}\ 5d^{10}\ 6s^2\ 6p^5$

Noble Gases

$Ne: 1s^2\ 2s^2\ 2p^6$

$Ar: [Ne]\ 3s^3\ 3p^6$

$Kr: [Ar]\ 3d^{10}\ 4s^2\ 4p^6$

$Xe: [Kr]\ 4d^{10}\ 5s^2\ 5p^6$

$Rn: [Xe]\ 4f^{14}\ 5d^{10}\ 6s^2\ 6p^6$

A bit trickier, but chalcogens and halogens also have a pattern.

Chalcogens have 6 valence electrons – 2 electrons away to form a closed shell.
Halogens have 7 valence electrons – 1 electron away to form a closed shell.
If they gain electrons such that they have 8 valence electrons, they will have the same electron configuration as that of noble gases, which is stable.

So, if those elements become ions, they will most likely be:

Chalcogen Ions:

$O^{2-}: [Ne]$

$S^{2-}: [Ar]$

$Se^{2-}: [Kr]$

$Te^{2-}: [Xe]$

$Po^{2-}: [Rn]$

Halides (Halogen Ions):

$F^-: [Ne]$

$Cl^-: [Ar]$

$Br^-: [Kr]$

$I^-: [Xe]$

$At^-: [Rn]$

We can also conclude the following:

Chalcogens usually have an oxidation state of -2.
Halogens usually have an oxidation state of -1.

It is important to note that, despite having ionic forms that are most likely to occur, some other seemingly less stable ionic forms may exist, so don’t get confused if we see an ion that doesn’t fit into our electron configuration predictions. Using this information, we can explain why ionic compounds (neutral compounds made from ions) have specific chemical formulae.

Ionic compounds need to maintain its neutral state. As a result, the charge from cations and anions need to cancel out.

For example:

- $Mg^{2+}$ has a charge of +2.
- $Cl^-$ has a charge of -1.
- To balance, we need 2 $Cl^-$ .

- $Na^+$ has a charge of +1.
- $Br^-$ has a charge of -1.
- To balance, we need 1 of each.

- $K^+$ has a charge of +1.
- $SO_4^{2-}$ has a charge of -2.
- To balance, we need 2 $K^+$ .

Here are some other ionic compounds that exist, alongside a table of polyatomic ions.

$NaCl$

$NaNO_3$

$Na_2O$

$Na_2CO_3$

$CaCO_3$

$Ca(OH)_2$

$CaCl_2$

$CaO$

$KBr$

$NH_4Cl$

$KMnO_4$

$KClO_3$

$BaSO_4$

$AlCl_3$

$Al_2O_3$

$CH_3COONa$

It’s basically a matching game, though some ionic compounds are more stable than others; some have low solubility; some are in an aqueous state in water, etc. We will talk about this in future units.

Transition Metals

We won’t be going through every transition metal because it’s too much to deal with. Instead, let’s talk about some transition metals that play major roles in our body. They are, with their respective electron configuration:

Chromium (24)
Manganese (25)
Iron (26)
Cobalt (27)
Copper (29)
Zinc (30)
Molybdenum (42)

$[Ar]\ 3d^5\ 4s^1$
$[Ar]\ 3d^5\ 4s^2$
$[Ar]\ 3d^6\ 4s^2$
$[Ar]\ 3d^7\ 4s^2$
$[Ar]\ 3d^{10}\ 4s^1$
$[Ar]\ 3d^{10}\ 4s^2$
$[Kr]\ 4d^5\ 5s^1$

Other important metals are sodium, magnesium, potassium, and calcium, which we have already discussed in the example above.

When we talk about metals inside our systems, we don’t actually mean the metal atoms themselves inside our systems – that would be catastrophic because some can be very reactive. What we mean is the metal ions inside our systems. Metal ions participate in a lot of biochemical molecules and mechanisms. So, let’s get ourselves more acquainted with them, starting with chromium.

Chromium $[Ar]\ 3d^5\ 4s^1$ can have an oxidation state of +3 and +6.

We can explain this using crystal field theory, which dives into the d- and f-block configurations. Recall that for the d subshell ( $l = 2$ ), there are 5 different orientations ( $m_l = -2, -1, 0, 1, 2$ ). Within those 5 orientations, we can actually separate them into 2 groups:

3 orientations that have slightly lower energy called the $t_{2g}$ orbitals.
2 orientations that have slightly higher energy called the $e_g$ orbitals.

$Cr (III)$ assumes a configuration of:

$[Ar]\ 3d^3$

This is stable because there are 3 electrons in the d subshell. Even though the d subshell is not fully filled or half-filled, the $t_{2g}$ orbitals are half-filled, making it stable.

$Cr (VI)$ assumes a configuration of:

$[Ar]$

This is stable because it is a closed shell configuration. However, it is slightly more unstable than $Cr^{3+}$ because it lost a lot of electrons to obtain this configuration.

We can see $Cr (VI)$ hiding in our polyatomic ion table in the form of $CrO_4^{2-}$ and $Cr_2O_7^{2-}$ .

Example 1: Chromium in Our Body

Although it requires more research, it is observed that chromium potentially participates in some form of the following:

Carbohydrate, lipid, and protein metabolism.
Insulin potentiation to control blood sugar contents.
Possible antioxidant effects.

Chromium supplements include chromium (III) picolinate. However, there is not enough research evidence to claim that chromium supplements help with sugar metabolism.

The molecular structure of chromium (III) picolinate. Attribution: Smokefoot, CC BY 4.0 https://creativecommons.org/licenses/by/4.0, via Wikimedia Commons

More information can be found here: https://ods.od.nih.gov/factsheets/Chromium-HealthProfessional/
Simplified information can be found here: https://ods.od.nih.gov/factsheets/Chromium-Consumer/

Manganese $[Ar]\ 3d^5\ 4s^2$ can have an oxidation state of +2, +4, and +7.

$Mn (II)$ assumes:

$[Ar]\ 3d^5$

This is stable because the d subshell is half-filled.

$Mn (IV)$ assumes:

$[Ar]\ 3d^3$

This is stable because the $t_{2g}$ orbitals are half-filled.

$Mn (VII)$ assumes:

$[Ar]$

This is stable because it’s a closed shell.

Example 2: Manganese in Our Body

Manganese has a more well-established correlation in our body. Its function includes:

Being cofactors in many enzymes (proteins that speed up chemical reactions in our body), including an enzyme that is essential in urea production.
Through these enzymes, participating in amino acid, cholesterol, glucose, and ROS (reactive oxygen species) metabolism.
In conjunction with vitamin K, playing a role in blood clotting.

Manganese peroxidiase (enzyme) reacts with ROS. Attribution: Acalgaro, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons

Manganese deficiency is very rare, so there isn’t a defined list of symptoms, as well as excess manganese intake.

More information: https://ods.od.nih.gov/factsheets/Manganese-HealthProfessional/
Simplified: https://ods.od.nih.gov/factsheets/Manganese-Consumer/

Iron $[Ar]\ 3d^6\ 4s^2$ can have an oxidation state of +2 and +3.

$Fe (II)$ assumes:

$[Ar]\ 3d^6$

Surprisingly, this is not stable and will oxidize to $Fe (III)$ under an oxidizing agent. However, without an oxidizing agent, it is very stable.

$Fe (III)$ assumes:

$[Ar]\ 3d^5$

This is stable because the d subshell is half-filled.

Example 3: Iron in Our Body

Iron is quite well researched. It is essential to our body, having the following functions:

Essential part of hemoglobin – a protein responsible for oxygen transportation in blood.
Essential part of myoglobin – a protein responsible for oxygen transportation to the muscles.
Necessary for physical growth, neurological development, cellular functioning, and some hormone synthesis.

Heme – the part of hemoglobin and myoglobin that contains iron – can bind and unbind oxygen. It contains Fe (II). Attribution: Smokefoot, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

Iron deficiency is well researched as well, considering how important it is in our body. Iron deficiency is also common in the world. In more severe cases, it can cause iron deficiency anemia (IDA). Anemia means “decreased presence of red blood cells in the blood”. IDA is observed to associate with:

gastrointestinal disturbances

weakness

fatigue

difficulty concentrating

impaired cognitive function

impaired immune function

impaired exercise or work performance

impaired body temperature regulation

etc.

Of course, excess iron intake can also cause problems. High-dose iron supplements can cause gastrointestinal effects, including gastric upset, constipation, nausea, abdominal pain, vomiting, and diarrhea.

More information: https://ods.od.nih.gov/factsheets/Iron-HealthProfessional/
Simplified: https://ods.od.nih.gov/factsheets/Iron-Consumer/

Cobalt $[Ar]\ 3d^7\ 4s^2$ can have an oxidation state of +2 and +3.

Unfortunately, electron configurations are not sufficient to explain this property. In fact, this is out of scope of this course.

Example 4: Cobalt in Our Body

Cobalt is essential in trace amounts but toxic in large amounts. In trace amounts, cobalt does the following:

It is a key constituent of cobalamin, a.k.a. vitamin B₁₂, which is involved in:
- DNA synthesis.
- Fatty acid and amino acid metabolism.
- Nervous system functioning.
- Maturation of red blood cells in the bone marrow.

The molecular formula for vitamin B₁₂. Public domain

The structure of cobalamin. The dark blue sections indicate cobalt. Public domain

$Co$ in vitamin B₁₂ usually exists as $Co (III)$ . Under reducing conditions, it can be reduced to $Co (II)$ and even $Co (I)$ . Also, vitamin B₁₂ is the only vitamin that must be sourced from animal-derived foods or supplements.

Cobalt deficiency is mostly characterized by cobalamin deficiency. This deficiency reflects in 3 of our systems: the circulatory system, nervous system, and digestive system.

More information: https://en.wikipedia.org/wiki/Vitamin_B12

Copper $[Ar]\ 3d^{10}\ 4s^1$ can have an oxidation state of +2.

This is interesting. We would think that, almost without doubt, Copper should have an oxidation state of +1 because it will land us with $[Ar]\ 3d^{10}$ – a fully filled subshell. However, $Cu^+$ is reactive with itself.

$2\ Cu^+ \rightarrow Cu + Cu^{2+}$

As a result, due to other reasons, $Cu (II)$ is the common one.

Example 5: Copper in Our Body

Copper is also a well-researched element. It has involves in the following:

Being cofactors in cuproenzymes that involve in energy production, iron metabolism, and neurotransmitter synthesis.
Angiogenesis – the generation_(genesis) of blood vessels_(angio-).
Neurohormone homeostasis – equilibrium_{(homeostasis)} of hormones in our nervous system.
Gene regulation, pigmentation, immune system functioning, etc.

The structure of an enzyme containing copper that catalyzes ROS. It has Cu (II) indicated as 2 of the colored balls. Attribution: Dcrjsr, CC BY 4.0 https://creativecommons.org/licenses/by/4.0, via Wikimedia Commons

The enzyme above is called a superoxide dismutase (SOD), which deals with superoxide ( $O_2^-$ , an ROS) to produce $H_2O_2$ – another ROS that will be degraded by catalase. The mechanism looks like this.

$Cu^{2+}\text{-SOD} + O_2^- \longrightarrow Cu^+\text{-SOD} + O_2$
$Cu^+\text{-SOD} + O_2^- + 2\ H^+ \longrightarrow Cu^{2+}\text{-SOD} + H_2O_2$

$O_2^-$ is a strong reducing agent because of the extra electron, reducing $Cu^{2+}$ to $Cu^+$ .

Copper deficiency can cause the following:

Anemia – without_(an-) red blood cells in the blood_(-emia)
Hypopigmentation – below normal_(hypo-) amounts of pigmentation
Hypercholesterolemia – above normal_(hyper-) amounts of cholesterol in the blood_(-emia)
Osteoporosis – a condition_(-osis) that makes bones_(osteo-) more porous
Ataxia – without_(a-) order_(taxia) (a neurological sign consisting of lack of voluntary coordination of muscle movements)

Excess copper consumption can lead to liver damage and gastrointestinal symptoms.

More information: https://ods.od.nih.gov/factsheets/Copper-HealthProfessional/
Simplified: https://ods.od.nih.gov/factsheets/Copper-Consumer/

Zinc $[Ar]\ 3d^{10}\ 4s^2$ can have an oxidation state of +2.

This is more predictable according to our electron configuration model. An oxidation state of +2 assumes a configuration of $[Ar]\ 3d^{10}$ , which is a fully filled subshell.

Example 6: Zinc in Our Body

We also know relatively a lot about zinc. Zinc is involved in the following:

Cofactors in numerous enzymes.
Enhancing immune functions.
Protein and DNA synthesis.
Cell signaling and division.

A zinc finger, a protein motif which can read DNA sequences, with Zn (II) as the sphere. Attribution: Thomas Splettstoesser (www.scistyle.com), CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

Zinc deficiency is also fairly common. It can affect our hair, skin, and bones and also digestive, reproductive, nervous, and immune systems. More specifically, it may cause the following:

Skin-related:
- Acne – clogged sebum
- Eczema – skin eruption
- Alopecia – hair loss
- Xerosis – a condition_(-osis) of dry_(xero-) skin

Mouth-related:
- Ulcer – open skin/epithelial wound
- Stomatitis – inflammation_(-itis) of the mouth_(stomato-)

High zinc intakes can cause nausea, dizziness, headaches, gastric distress, vomiting, and loss of appetite.

Let’s also talk about zinc and the immune system.

Too little zinc may lead to overproduction of immune cells.
Too much zinc may suppress immune function.

More information: https://ods.od.nih.gov/factsheets/Zinc-HealthProfessional/
Simplified: https://ods.od.nih.gov/factsheets/Zinc-Consumer/

Molybdenum $[Kr]\ 4d^5\ 5s^1$ can have an oxidation state of +4 and +6.

Our electron configuration model is insufficient to explain the +4 oxidation state. For +6, it’s because it yields a closed shell configuration. We can see $Mo (VI)$ in action in the form of the polyatomic ion molybdate $MoO_4^{2-}$ .

Example 7: Molybdenum in Our Body

Molybdenum is another trace element that is essential. It is involved in:

A structural constituent in enzymes that metabolize sulfur-containing amino acids.
A structural constituent in enzymes that metabolize drugs and toxins.

A molybdenum cofactor in Mo-dependent enzymes with Mo having an oxidation state of +6. Public domain

More information: https://ods.od.nih.gov/factsheets/Molybdenum-HealthProfessional/
Simplified: https://ods.od.nih.gov/factsheets/Molybdenum-Consumer/

Break Time: 10 Minutes

Take a short break!

This break time features composer Nikolai Kapustin (1937-2020), a Soviet composer and pianist of Russian-Jewish descent. He is known for his fusion of classical music and jazz, especially from his conservatory training in the Moscow Conservatory, which is very different from the likes of Gershwin (mostly self-taught) and other jazz legends such as John Coltrane and Ornette Coleman.

This recording is performed by Kapustin himself!

Lecture Content (Part 2)

This part of the lecture will focus on how electron configurations can affect the properties of elements, including their size, affinity to electrons, reactivity, etc.

Periodic Table Trends

Periodic table trends can be explained by the interaction between the negatively charged electrons and the positively charged nucleus. This interaction can be summarized by one equation.

This equation is called Coulomb’s Law, which gives us an idea of the attractive force between the electrons and the nucleus.

(1) $\begin{equation*} F = k\ \frac{q_e q_n}{r^2} \end{equation*}$

which:

$F$ denotes the attractive force.

$k$ denotes a constant.

$q_e$ denotes the charge of an electron of our choice.

$q_n$ denotes the charge of the nucleus, which increases as we go up the periodic table.

$r$ denotes the distance between the electron of our choice and the nucleus.

Atomic Radius

Recall that valence electrons are important in element reactivity. As a result, how far they are ( $r$ ) from the nucleus can determine how easy those electrons can leave the element. Similarly, it can also determine how easy other electrons can join the element.

Here are the data and trends. (Access the data here)

This diagram contains the trend lines for elements 1-86. The data is from Wikipedia. (made in MS Excel)

Trend 1: Provided the same group, higher period generally means bigger radius.
- Higher period essentially means the valence electrons have a bigger $n$ value, which means they’re farther away from the nucleus. Since they are farther from the nucleus, the valence electrons of elements with the same group number but a higher period will be less attracted to the nucleus.

(2) $\begin{equation*} k\ \frac{q_e q_n}{r^2 \uparrow}\longrightarrow F\downarrow \end{equation*}$

For example, $K$ (period 4, group 1) has a bigger radius than $Na$ (period 3, group 1), and $I$ (period 5, group 17) has a bigger radius than $Br$ (period 4, group 17).

Trend 2: Provided the same period, especially in the s- and p-blocks, higher group number means smaller radius.
- If elements are in the same period, they have the same $n$ value for their outermost electrons. However, as the elements go through the periodic table, their atomic number increases, meaning that they have more protons. More protons mean a higher nuclear charge, which means bigger attractive force. Bigger attractive force means that the valence electrons will be closer to the nucleus compared to other elements with the same period but a smaller group number.
- However, this trend gets less reliable when the d- and f-block elements are involved.

(3) $\begin{equation*} k\ \frac{q_e q_n \uparrow}{r^2}\longrightarrow F\uparrow \longrightarrow k\ \frac{q_e q_n}{r^2 \downarrow}\end{equation*}$

For example, $Ca$ (period 4, group 2) has a bigger radius than $Fe$ (period 4, group 8), and $O$ (period 2, group 16) has a bigger radius than $F$ (period 2, group 17).

Trend 3: Provided the same period, especially in the d- and f-blocks, higher group number can also lead to bigger radius.
- The d- and f-blocks have more valence electrons (recall our quantum theory of electrons) in the d and f subshells. So, as we move to the right of the periodic table, the filling of the d and f subshells means that there are more electrons in the inner shells, allowing more repulsion from the inner shells. As a result, the outer shell electrons may be repelled to a farther distance.
- This trend conflicts with the nuclear charge trend (Trend 2). However, in most cases, Trend 2 dominates.

We can summarize those 3 trends into the following table.

Factor

Principle

If…

Means…

Atomic Radius

Electron Shell

Quantum numbers

Increase in the principle quantum number

Increase down each column

Increase

Nuclear Charge

Coulomb’s Law – attraction between electrons and nucleus

Increase in atomic number

Increase along each row

Decrease

Electron Repulsion

Coulomb’s Law – repulsion between inner shell electrons and outer shell electrons

Increase in atomic number (in d- and f-blocks)

Reduce the effect of nuclear charge

Increase

Those 3 factors compete with each other to determine how the atomic radii work.

Ionic Radius

Recall that ions are formed from atoms gaining or losing electrons. We went through the ions that can be formed from a selection of elements. Since they gain or lose electrons, the radii of the ions will be different. However, the trend will be slightly different from that of the atomic radii.

The radii are influenced by 2 factors – electron shell and electron repulsion.
Nuclear charge is not considered because ion formation does not change the atomic number of the element.

As a result, if an element loses electrons and becomes a cation, its radius will decrease – there is less repulsion among valence electrons, leading to a smaller radius. In addition, the ion can lose an entire shell, further decreasing the radius.

Similarly, if an element gains electrons and becomes an anion, its radius will increase – there is more repulsion, leading to a larger radius. Remember, since the atomic number stays the same, there will be no stronger attractive force.

For example:

$K$ has a bigger radius than $K^+$ because $K^+$ does not have electrons in the 4th shell.
$O^{2-}$ has a bigger radius than $O$ because $O^{2-}$ has more valance electrons, causing more repulsion.

Here is a brief summary.

Factor

Principle

If…

Means…

Radius

Electron Shell

Quantum numbers

Increase in the principle quantum number

Increase down each column

Increase

Electron Repulsion

Coulomb’s Law – repulsion among valance electrons

Gain in electrons while maintaining the same atomic number

Reduce the effect of nuclear charge (which is constant)

Increase

Effective Nuclear Charge

The effective nuclear charge is denoted by $Z_{eff}$ (we will call it “Zeff”). Recall that in our atomic radius trend, we talked about how nuclear charge and electron repulsion are conflicting factors:

As the atomic number increases, there is more nuclear charge, decreasing the radius.
As the atomic number increases, there is more electron repulsion, increasing the radius.

Essentially, electron repulsion can cancel the effects from nuclear charge. As a result, we want to know what the actual impact of nuclear charge on electrons is – what is the actual force of attraction from the nucleus when we take electron repulsion into account?

Effective nuclear charge $Z_{eff}$ is basically the actual nuclear charge with electron repulsion factored in. It is reflected in the formula.

(4) $\begin{equation*} Z_{eff} = Z - S \end{equation*}$

which:

$Z_{eff}$ is the effective nuclear charge of an electron

$Z$ denotes the atomic number of the element

$S$ denotes the shielding constant (a fancy way of saying quantified electron repulsion)

Exactly how $S$ is calculated is out of scope.

We can conclude that:

Higher Zeff

means

Less shielding effect

Lower Zeff

means

More shielding effect

For each electron in a particular subshell, it has a unique Zeff value. For example, let’s look at the elements in period 4.

Observe that, within the same period:

Provided the same subshell, higher atomic number means higher Zeff.
Provided the same atomic number, outer orbitals mean smaller Zeff.

The Zeff of different orbitals in period 3. “Z” denotes the atomic number. Source: https://en.wikipedia.org/wiki/Effective_nuclear_charge

Let’s look at the trend. Below is a diagram of the Zeff values for electrons in the outermost orbitals for elements 1-54.

The Zeff for valence electrons for elements 1-56. The data is from Wikipedia. (made in MS Excel)

We will focus on valence electrons here because, again, valence electrons are responsible for reactivity.

Trend 1: Provided the same group, higher period generally means higher valance electron Zeff.
Trend 2: Provided the same period, higher group number generally means higher valence electron Zeff.
- This provides another explanation on why atomic radii decrease as we go along a period – since Zeff increases as we go along a period, there is less shielding effect on the electrons, decreasing the atomic radii.
- This also provides another explanation on why anions have a larger radius than its neutral form – since the atomic number stays the same and there is more shielding effect from the extra electrons, Zeff decreases, which increases the anion’s radius.
- This also provides another explanation on why cations have a smaller radius than its neutral form.

Factor

Principle

If…

Means…

Zeff

Nuclear Charge

Coulomb’s Law – attraction between electrons and nucleus

Increase in atomic number

More coulombic attraction

Increase

Shielding Effect (Electron Repulsion)

Coulomb’s Law – repulsion between inner shell electrons and outer shell electrons

Increase in atomic number

Reduce the effect of nuclear charge

Decrease

Note: Zeff does not factor distance into the equation. It only factors in the charge.

Ionization Energy

Ionization energy answers one question:

What is the energy required to knock 1 electron out of an atom?
In other words, how easy is this element to lose 1 electron?

In a redox reaction, the easier it is to lose an electron, the stronger it is to be a reducing agent (or the easier it is to be oxidized). We have figured out how to quantify the energy by forcing the element to lose an electron and measure the energy required.

The ionization energy ( $\text{IE}$ ) is the minimum energy required to remove the most loosely bound electron of an isolated gaseous atom, positive ion, or molecule. The energy required to remove the first electron is called the $\text{1st IE}$ . In terms of chemical reaction, the $\text{1st IE}$ looks like the following:

(5) $\begin{equation*} X(g) + \text{1st IE}\longrightarrow X^+(g) + e^- \end{equation*}$

which:

$X$ denotes any gaseous atom, positive ion, or molecule

$\text{1st IE}$ denotes the first ionization energy

$e^-$ denotes an electron

Let’s look at the trend.

Green – s-block; Yellow – p-block; Blue – d-block. The data is from Wikipedia. (made in MS Excel)

The trend can explained quantitatively by Coulomb’s Law:

(6) $\begin{equation*} F = k \frac{q_eq_n}{r^2} \end{equation*}$

The higher the $F$ for the outermost electron is, it requires higher energy to remove that electron, which corresponds to a higher $\text{1st IE}$ value. This trend can also be qualitatively explained by 2 factors:

Factor

Principle

If…

Then…

Thus…

Zeff

Coulomb’s Law – Charge

Increase

$F$ increases

$\text{1st IE}$ increases

Atomic Radius

Coulomb’s Law – Distance

Increase

$F$ decreases

$\text{1st IE}$ decreases

Here are the trends:

Trend 1: Provided the same group, higher period generally means lower .
- Zeff increases because it has a higher period.
- Atomic radius increases because it has a higher period.
- Theoretically, we don’t know how $\text{1st IE}$ will change. But, the atomic radius increases a lot, which dominates the change in this case.

Trend 2: Provided the same period, higher group number generally means higher .
- Zeff increases because it has a higher group number.
- Atomic radius decreases slightly because it has a higher group number.
- Those 2 factors combined yields an increasing $\text{1st IE}$ .

We can see a huge exception and a small exception in our trend from the diagram:

Exception 1: The major drop in from the d-block elements to the p-block elements.
- It can be explained by electron configurations. Once we transition from the d-block elements to the p-block elements, we start filling the orbitals from d subshells to p subshells of a higher shell – a relatively big increase in distance, decreasing $\text{1st IE}$ .

Exception 2: There is a little dip in the middle of the some p-block elements. More specifically: , ,
- It can be explained by electron configurations again. $N, P, As$ all have electron configurations with a half-filled p subshell. As a result, it’s stable and will be harder to knock an electron off compared to the ones after them.
- This exception dominates less as we go down the periodic table.

Electron Affinity

Electron affinity answers a completely opposite question. Rather than forcing an electron away, what is the energy released if we add an electron onto a neutral atom or a molecule.

In a redox reaction, the easier it is to add an electron, the better it is to be an oxidizing agent (or the easier it is to be reduced). Similar (yet quite opposite) to ionization energy, we have a way to measure it.

Electron affinity $E_{ea}$ is the amount of energy released when an electron attaches to a neutral atom or molecule in the gaseous state to form an anion.

(7) $\begin{equation*} X(g) + e^- \longrightarrow X^-(g) + E_{ea} \end{equation*}$

which:

$X$ denotes any gaseous atom or molecule

Let’s look at the trends.

Some data points are not available because it actually requires energy to add that electron in, which is very difficult to do, and the resulting anion is very unstable that it’s hard to monitor. As we can see, it’s not as easy to find a trend. But we can still explain some trend using our 2 friends – Zeff and atomic radius.

Factor

Principle

If…

Then…

Thus…

Zeff

Coulomb’s Law – Charge

Increase

$F$ increases

$E_{ea}$ increases

Atomic Radius

Coulomb’s Law – Distance

Increase

$F$ decreases

$E_{ea}$ decreases

Trend 1: Provided the same group number, higher period sometimes means lower .
- It’s not a very universal trend, but we can see the halogens decrease in $E_{ea}$ except $F$ because $F$ has a small radius such that there is more shielding effect, decreasing $E_{ea}$ .
- We will occasionally reference this trend, but since it’s not as obvious, data would likely be provided.

Trend 2: Provided the same period, higher group number generally means higher .
- Zeff increases and atomic radius decreases slightly, leading to higher $E_{ea}$ .
- The exception that half-filled p subshells have a low $E_{ea}$ still stands.

Electronegativity

Electronegativity is a very important concept that will pop up again and again in this chapter. In a way, electronegativity describes something kind of the opposite of ionization energy and something similar to electron affinity, but is different enough to warrant itself as a separate concept and trend.

Electronegativity $\chi$ is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond.

(8) $\begin{equation*} |\chi_A - \chi_B| = \sqrt{E_d(AB) + \frac{E_d(AA) + E_d(BB)}{2}} \end{equation*}$

which:

$\chi$ denotes electronegativity

$A, B$ denote individual elements

$AB, AA, AB$ denote formed molecules

$E_d$ denotes dissociation energy – the energy required to break the bonds within the molecule

We set $\chi_H$ (the electronegativity of hydrogen) to be 2.20.
We also omit the units for this property as a convention.

The formula essentially quantifies the observation that if we have atoms A and B, the bond formed in $AB$ is larger than that in $AA$ or $BB$ . This observation means that, in a molecule, some atoms attract electrons to them more strongly, forming a stronger bond.

So, electronegativity doesn’t describe electrons being gained or lost (basically, an ionic perspective). In fact, it describes electrons being more or less likely around that atom inside a molecule without actually gaining or losing electrons (basically, a molecular perspective, not an ionic one). We will see that in action more in the next lecture.

Consequently:

Ionization energy and electron affinity focus more on elemental reactivity or reactivity of ionic compounds, especially when it comes to redox reactions.
Electronegativity focuses more on molecular reactivity. It doesn’t say much for individual atoms or ions – only when those atoms are connected through covalent bonds (see the next lecture and organic chemistry).

Here’s a diagram of the trend.

Green – s-block; Yellow – p-block; Blue – d-block. Available noble gases data is dotted. The data is from Wikipedia. (made in MS Excel)

We can observe a clearer trend from this diagram (bar the d-block elements).

Factor

Principle

If…

Then…

Thus…

Zeff

Coulomb’s Law – Charge

Increase

$F$ increases

$\chi$ increases

Atomic Radius

Coulomb’s Law – Distance

Increase

$F$ decreases

$\chi$ decreases

Trend 1: Provided the same group, higher period generally means lower electronegativity.
- Explanation: higher Zeff and larger atomic radius with dominating atomic radius effects.

Trend 2: Provided the same period, higher group number generally means higher electronegativity.
- Explanation: higher Zeff and slightly smaller atomic radius.

Electrons and Chemical Reactivity

We talked a lot in this lecture. To summarize:

Electrons in an element have specific configurations.
Those configurations influence the element’s ability to lose ( $\text{IE}$ ), gain ( $E_{ea}$ ), or simply attract ( $\chi$ ) electrons.
The combination of those abilities influence how those elements (and as we go on) and molecules interact with others, paving a way to understand biochemical reactions.

So, here are some examples.

Metal Reactivity

Here is a list of different metals reacting with water, which is not a strong oxidizing agent. Using this, we can gauge how strong a metal is as a reducing agent.

We will order this list from strong to weak, with the following redox reaction in mind.

For alkali metals, we have:

$2\ M + 2\ H_2O \longrightarrow 2\ MOH + H_2\uparrow$

For alkaline earth metals, we have:

$M + 2\ H_2O \longrightarrow M(OH)_2 + H_2\uparrow$

For transition metals, we have a mix of reactions above (or lack of) depending on the oxidation state or reactivity of said metal.

Observing the reaction, we can conclude that, in the reactions above:

The metal is oxidized and acts as a reducing agent (its oxidation state changes from 0 to +1/+2/+3).
Water is reduced and acts as an oxidizing agent (hydrogen changes from +1 to 0).

In a way, the metal loses electron(s) and transfers the electron(s) to water, forming a base and hydrogen gas in the process. To see how eager the metal is willing to lose electron(s), we observe how intense the reaction is.

Let’s start with the most reactive ones – the alkali metals.

$2\ M + 2\ H_2O \longrightarrow 2\ MOH + H_2\uparrow$

Metal

Reaction

1st IE (kJ/mol)

$Cs$

Explosion and ignition of $H_2$ if cesium didn’t fly off immediately

375.7

$Rb$

Explosion and ignition of $H_2$

403.0

$K$

Strong reaction and ignition of $H_2$ , possible explosion

418.8

$Na$

Strong reaction and ignition of $H_2$

495.8

$Li$

Strong reaction and possible ignition of $H_2$

520.2

Alkaline earth metals follow suit, slightly less reactive than alkali metals in general because a second electron needs to be knocked off as well.

$M + 2\ H_2O \longrightarrow M(OH)_2 + H_2\uparrow$

$Ba$

Strong reaction and fizzling

502.9

$Sr$

Strong reaction and fizzling

549.5

$Ca$

Strong reaction with fizzling

589.8

$Mg$

Requires heat or gaseous water

737.7

$Be$

Requires gaseous water

899.5

Here’s an honorary metal – $Al$ , which requires gaseous water to react, and has a $\text{1st IE}$ of 577.5 kJ/mol. It’s less reactive because it needs to shed off 3 electrons.

Transition metal reactivity gets a bit complicated because other factors (out of scope) play a significant role in how those metals react. For reference, here’s the list of important metals in the body with some comments.

Metal

Ion

Comments

$Mn$

$Mn^{2+}$

Reacts with acids

$Zn$

$Zn^{2+}$

$Cr$

$Cr^{3+}$

$Fe$

$Fe^{2+}$

$Co$

$Co^{2+}$

$Cu$

$Cu^{2+}$

Cannot react with most acids

The metal reactivity series will be provided in most cases. The important concept here is to know how electron configuration can influence reactivity. In this case, we explored how electron configuration can help determine electron affinity, which, in turn, influence the reactivity of alkali and alkaline earth metals.

Acidity and Basicity

Recall back in Lecture 4, we introduced the concepts of acids and bases. Here’s a quick recap.

An acid is a substance that donates protons.
A base is a substance that accepts protons.

Using electron configurations, we can figure out which substances are better at donating or accepting protons. More specifically, let’s talk about how electronegativity and atomic radius can influence acidity.

Factor

If…

Then…

Thus…

Electronegativity

Higher electronegativity

Once the proton is donated, the anion is more stable, making the proton easier to leave

Higher acidity

Atomic radius

Bigger atomic radius

Smaller attraction to the proton (Coulomb’s Law), making it easier to leave

Higher acidity

Using this, let’s look at the following examples.

$HF < HCl < HBr < HI$

Electronegativity decreases, which means that $HF$ should’ve been the strongest acid.
However, atomic radius increases a lot, which dominates over the effects of electronegativity.

$CH_4 < NH_3 < H_2O < HF$

Atomic radius slightly decreases, which means that $CH_4$ should’ve been the strongest acid.
However, electronegativity increases, which dominates over the effects of electronegativity.

The reactivity of a substance is determined by a combination of factors working together or against each other. The final result looks at which factors dominate over others.

Summary

This is quite a heavy lecture – a lot of concepts are discussed. Let’s summarize.

Electrons are important in reactivity. How electrons are arranged can determine how atoms and ions react.

We can describe how electrons are arranged by their quantum numbers.
$n$ describes the shell

$l$ describes the subshell

$m_l$ describes the orientation

$m_s$ describes the spin

Using those quantum numbers, we can also visualize how electrons are distributed in an atom using electron configurations.
The electron configurations follow 3 rules: the energy rule, the exclusion rule, and the single occupancy rule.

Exceptions exist, mainly in the d- and f-block elements.

Using electron configurations, we can predict favorable ion formation and oxidation states of an element.
Alkali metals +1

Alkaline earth metals +2

Pnictogens -3

Chalcogens -2

Halogens -1

Transition metals, etc.

Patterns in electron configuration can be reflected in periodic table trends.
Number of valance electrons

Atomic and ionic radius

Effective nuclear charge $Z_{eff}$

Ionization energy $\text{IE}$

Electron affinity $E_{ea}$

Electronegativity $\chi$

Patterns in periodic table trends can be reflected in reactivity.
Metal reactivity

Acidity

etc.

Assignments

1. Preview Questions

What is Chapter 2 of this course about?
How are electrons arranged in an atom?
What are electron configurations, how do we determine them, and how are they important?
What are some periodic table trends and why should we know these trends?

2. Lecture Worksheet (TBD)

The lecture worksheet is available as a pdf file below. Remember, practice makes perfect!

3. Further Reading

Medical usage of noble gases: https://pmc.ncbi.nlm.nih.gov/articles/PMC2945072/
This paper does require more advanced knowledge in biochemistry and neurobiology. However, it is an interesting paper detailing how noble gases can be used as anesthesia and even neuroprotectants.

You finished the lecture! It’s a long lecture, so let’s take a break for today – it takes time for our brain to fully absorb new materials. Don’t forget to review!

Project MEEP

General Chemistry